Dijkstra’s Algorithm —

In this article we are going to understand one of the most popular distance finding algorithm with non-negative edge weights in Graph.

(Source: Wikipedia)

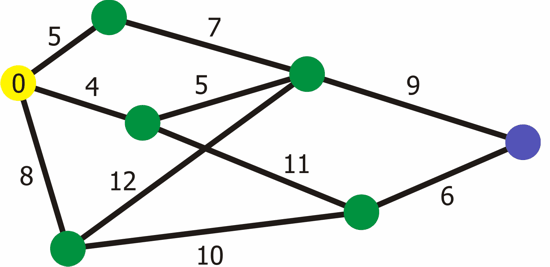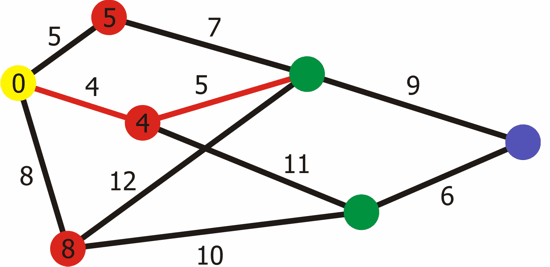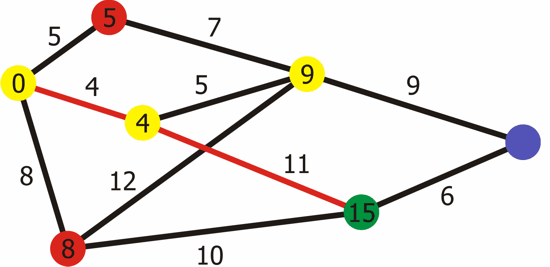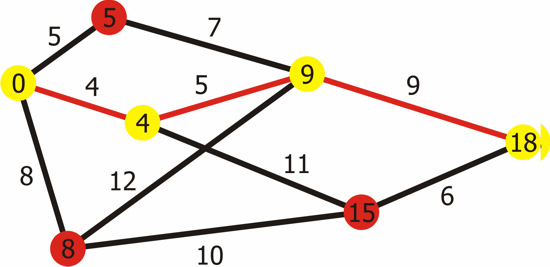
Problem Statement:

Given a weighted graph G with vertices V and edges E, and a source vertex s, the goal is to find the shortest paths from the source vertex s to all other vertices in the graph.

Algorithm Steps:

1. Initialization:

   • Initialize a distance array dist[] where dist[i] represents the distance from the source vertex to vertex i.

   • Set dist[s]=0 and dist[v]=∞ for all other vertices v.

   • Create a priority queue (or min-heap) to store vertices and their current distances. Enqueue the source vertex with distance 0.

2. Main Loop:

   • While the priority queue is not empty, do the following:

     • Dequeue the vertex u with the minimum distance from the priority queue.

     • For each neighboring vertex v of u, calculate the total distance from the source to v through u. If this distance is smaller than the current known distance to v, update dist[v] and enqueue v with the new distance.

3. Termination:

   • Once the priority queue is empty, the algorithm terminates, and the dist[] array contains the shortest distances from the source to all other vertices.

V - Destination U - source

#include <bits/stdc++.h>
using namespace std;

        // ∞ 
const int INF = numeric_limits<int>::max();
// You can put the any large value at the place of infinite such as 
// Maximum value of Integer.

class Graph {
private:
    int numNodes;
    vector<vector<pair<int, int>>> adjacencyList;

public:
              //constructor for the Graph class
    Graph(int n) : numNodes(n), adjacencyList(n) {}


    // Function to add an edge to the graph  u- source  v-destination 
    void addEdge(int source, int destination, int weight) {

         // Uncomment for undirected graph
        adjacencyList[source].push_back({destination, weight});
        adjacencyList[destination].push_back({source, weight});  
    }

    // Function to perform Dijkstra's algorithm
    void dijkstra(int start) {
        // Priority queue to store nodes and their distances
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;

        // Vector to store distances from the start node
        vector<int> distance(numNodes, INF);

        // Set the distance of the start node to 0
        distance[start] = 0;

        // Add the start node to the priority queue
        pq.push({0, start});

        while (!pq.empty()) {
            int u = pq.top().second;
            pq.pop();

            for (const auto& edge : adjacencyList[u]) {
                int v = edge.first;
                int weight = edge.second;

                // Relaxation step
                if (distance[u] + weight < distance[v]) {
                    distance[v] = distance[u] + weight;
                    pq.push({distance[v], v});
                }
            }
        }

        // Print the distances from the start node
        cout << "Shortest distances from node " << start << ":\n";
        for (int i = 0; i < numNodes; ++i) {
            cout << "To node " << i << ": " << (distance[i] == INF ? "INF" : to_string(distance[i])) << "\n";
        }
    }
};

int main() {

   Graph graph(6);

    // Adding edges to the graph U = 0,V = 1,W = 2(weight on a edge).. 
    graph.addEdge(0, 1, 2);
    graph.addEdge(0, 2, 4);
    graph.addEdge(1, 2, 1);
    graph.addEdge(1, 3, 7);
    graph.addEdge(2, 4, 3);
    graph.addEdge(3, 4, 1);
    graph.addEdge(3, 5, 5);
    graph.addEdge(4, 5, 2);

    // Starting node for Dijkstra's algorithm
    int startNode = 0;

    // Perform Dijkstra's algorithm using class and object
    graph.dijkstra(startNode);
    return 0;
}

Output

Shortest distances from node 0:
To node 0: 0
To node 1: 2
To node 2: 3
To node 3: 9
To node 4: 6
To node 5: 8

Dijkstra's algorithm is widely used in various applications

Airline Flight Path Planning:

• Airlines use Dijkstra's algorithm to determine the most cost-effective flight paths, taking into account factors such as fuel consumption, airspace restrictions, and flight times.

Routing Protocols in Computer Networks:

• Dijkstra's algorithm is often used in computer networking protocols like OSPF (Open Shortest Path First) and IS-IS (Intermediate System to Intermediate System) to find the shortest path between routers.

Traffic Engineering

Supply Chain Management

Time Complexity:

The time complexity of Dijkstra's algorithm depends on the data structures used for priority queue operations. With a simple array implementation or a binary heap, the time complexity is O((V+E)log⁡V).

Thank you for reading my content. Be sure to follow and comment on what you want me to write about next 🤓